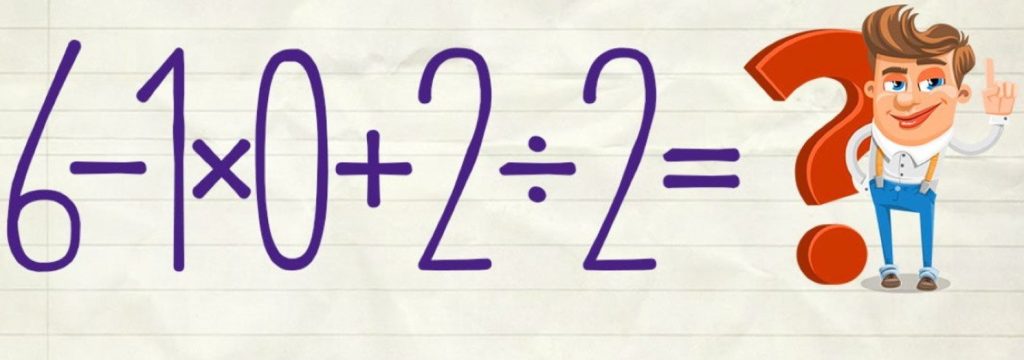Obsah článku
Dnes pro vás máme dvě velmi odlišné, ale velmi zajímavé hádanky, které zvládnou vyřešit jen ti, kterým matematika vždy šla. Je to dobrý způsob, jak se otestovat a zjistit, jestli je váš mozek rychlý a schopný řešit záludné otázky.
MATEMATICKÉ HÁDANKY
Tento zdánlivě jednoduchý matematický příklad vyvolal na internetu vlnu diskusí. Je to proto, že odpovědi se u jednotlivých čtenářů lišily. Někteří z nich si byli jisti, že správná odpověď je 5. Jiní byli přesvědčeni, že výsledek by měl být jeden. Ostatní trvali na tom, že správná odpověď je 7. Kdo měl pravdu? Nebo je odpověď úplně jiná?
Odpověď
Při řešení tohoto příkladu si musíme vzpomenout na školní pravidlo, že nejprve provedeme násobení a dělení a teprve potom sčítání a odčítání. Pokud ano, bude mít náš příklad následující podobu:
6 – 1 * 0 + 2 / 2 = 6 – 0 + 1 = 7.
Pokud jste snadno uhodli první z nich, tady je další, kde musíte logicky přemýšlet
Kdysi dávno prý sultán Saladin zajal jednoho rytíře. Vládce řekl, že vězně i s koněm propustí, pokud dostane slušné výkupné ve výši 30 000 zlatých. Rytíř neměl peníze ani bohaté příbuzné, a tak se rozhodl podvádět.
„Ó mocný Saladine, nedává mi žádnou naději. V mé vlasti má každý chytrý vězeň šanci dostat se na svobodu. Nabídnou mu skládačku. Pokud ji vyřeší, bude volný, pokud ne, výkupné se zdvojnásobí,“ řekl rytíř.
Saladin miloval hlavolamy, a tak se mu vězňův návrh zamlouval.
Zadání
„Dobrá, budiž. Zde je vaše hádanka. Zítra ráno dostanete dvanáct stejně vypadajících mincí a jednoduchou váhu bez závaží. Jedna mince bude falešná. Nikdo však neví, zda je lehčí nebo těžší než ostatní. K určení, zda se jedná o padělek, budete mít tři vážení. Pokud se vám to nepodaří, prohrál jste!
Jak můžete najít padělek mezi 12 mincemi při třech váženích? A je to vůbec možné?

Řešení druhého problému bude trvat déle
Situaci komplikuje skutečnost, že nevíme, která mince je těžší: zda padělek, nebo pravá. Není také známo, zda se rytíři podařilo najít odpověď do rána. Zkusme to udělat za něj.
Nejprve rozdělte mince na tři stejné hromádky po čtyřech mincích. Na váze zvážíme první dvě sady mincí. Pokud mají stejnou hmotnost, pak máme štěstí a falešná mince je právě na třetí hromádce.
Poté zvážíme dvě libovolné pravé mince (libovolné z první a druhé hromádky) a dvě mince z poslední hromádky, kde se skrývá jedna falešná mince. Pokud váha opět ukáže rovnost, pak je padělanou mincí jedna ze zbývajících dvou (těch, kterých jsme se nedotkli).
Proto ve třetím kroku zvážíme jednu ze skutečných mincí, kterou již známe, s některou ze dvou zbývajících mincí. Pokud je opět stejná, pak je falešná mince ta, které jsme se nedotkli. Pokud se nerovná, je nalezen také padělek. Zjistíme také, zda je těžší nebo lehčí než originál.
V případě nerovnosti při druhém vážení se najde dvojice s padělkem. Najít falešnou minci nad třetím vážením opět není obtížné.
Pokud byla při prvním vážení jedna skupina těžší, znamená to, že mezi těmito prvními osmi mincemi je padělek. Možná by v tomto případě bylo lepší všechny mince očíslovat: první hromádka (těžká) – 1,2,3,4; druhá (lehká) – 5,6,7,8; třetí (skutečná) – 9,10,11,12.
Ve druhém kroku zvážíme mince 1,9,10,11 a 2,3,4,5. Pokud se rovná, pak jsou 6,7 nebo 8 nepravdivé. Zároveň jsme již po prvním vážení zjistili, že druhá várka je lehčí. Padělek je tedy světlejší než originál. Takže vážíme 6 a 7. Ta lehčí je padělek. Pokud se rovnají, padělaná mince má hodnotu 8.
Pokud jsme po druhém kroku zjistili, že skupina 1,9,10,11 je těžší než skupina 2,3,4,5, pak je padělek buď 1 (těžší), nebo 5 (lehčí). Stačí zvážit například 1 a jakoukoli skutečnou minci. Pokud je 1 těžší, pak je falešná. Pokud se rovná, jedná se o falešnou pětku.
Pokud se ukáže, že mince 2,3,4,5 je těžší, znamená to, že padělaná mince je těžší a je mezi mincemi 2,3,4. V tomto případě zvažte například 2 a 3. Těžší je ten falešný. Pokud se rovnají, je padělaná mince číslo 4.
To poslední nebylo snadné. Samozřejmě byste to mohli zjednodušit změnou původních podmínek, ale bylo by to spravedlivé? Doufám, že to rytíř také dokázal vyřešit, protože měl zřejmě větší motivaci. Nebo snad existoval jednodušší způsob, který našel?